n個の中から重複を許してr個を選んで取り出す、組合せの総数を計算します。

全体の数(n個)と選んだ数(r個)を入力し「組合せを計算」ボタンをクリックすると、n個の中から重複を許してr個を選んで、取り出す組合せの総数を計算して表示します。

また、組合せの総数を求める計算方法も表示します。

全体の数と選んだ数は10,000までの正の整数で入力してください。

組合せとは、区別可能な異なるものの中から、いくつかを選んで取り出すことです。

重複を許して選んで取り出した組合せを組合せといいます。

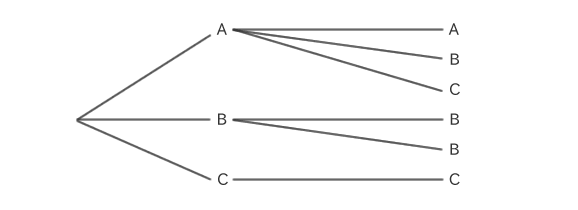
例えば、A、B、Cの3つのアルファベットから、2つを選ぶとします。

同じものを複数回選ぶことも出来るので、このときの選び方は、「AA、AB、AC、BB、BC、CC」の6通りになります。

組合せでは順列と違って順番を考えないので、ABとBAといった並び替えて同じになる組合せは1つとして考えます。

A、B、Cから2つを選んだ場合の組合せを樹形図にするとこのようになります。

重複組合せの総数を計算する場合、丸と仕切りを使って考えます。

例えば、A、B、Cの3つのアルファベットがあり、この中から4つを選んで組合せを考えるとします。

選ぶ4つのアルファベットを丸(〇)とし、アルファベットの種類が3種類なので仕切り(｜)を2つ用意して並べます。

丸と仕切りを並べて、仕切りの左からABCとします。

例えば、〇〇｜〇｜〇の場合は、AABCの組合せとなります。また、〇｜｜〇〇〇の場合は、ACCCの組合せとなります。

この丸と仕切りの順列の総数が、重複組合せの総数になります。

丸と仕切りの順列の総数は6!で、丸と仕切りはそれぞれ区別がないので(4! × 2!)で割ります。

なので、組合せの総数は 6!4!2! = 15 になります。

よって、n個からr個を重複を許して選んで取り出した組合せの総数は(r+n−1)!r!(n−1)!で計算できます。