n個のものを円形に並べたときの、並べ方の総数を計算します。

全体の数(n個)と選んだ数(r個)を入力し「円順列を計算」ボタンをクリックすると、異なるn個のものを円形に並べたときの並べ方の総数を計算して表示します。

また、並べ方の総数を求める計算方法も表示します。

並べる数は10,000までの正の整数で入力してください。

順列とは、区別可能な異なるものの中からいくつかを選んで、一列に並べた列のことです。

円順列は、選んだものを円形に並べた列のことです。円順列の場合は、回転させて同じものは1通りとして数えます。

例えば、A、B、Cの3つのアルファベットを円形に並べるとします。

順列の場合は並べ方は6通りになりますが、円順列の場合は回転させて同じものは1通りなので、ABCとBCAとCABなども1通りとして数えます。

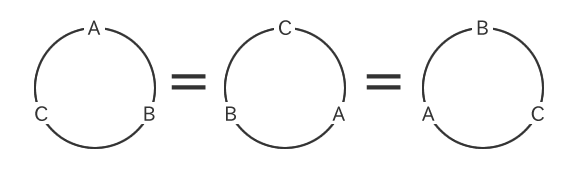
このときの並べ方は、「ABC、ACB」の2通りになります。

円順列で並べ方の総数を計算する場合、回転して同じになるものは1通りになるので、一つの場所を固定して考えていきます。

一つの場所を固定することで、回転を考えずに残りを順列として考えることで総数を計算することができます。

例えば、A、B、C、Dの4つのアルファベットを円形に並べるとします。

一番上をAと固定すると、残り3個の順列になります。

よって、並べ方の総数は3! = 3×2で6通りになります。

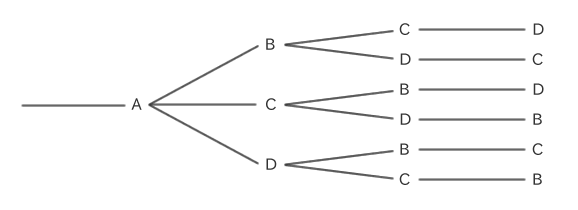
このように、円順列の並べ方の総数は、全体の数(n個)から1を引いた数の順列になります。

よって、円順列の公式は以下のようになります。