異なるn個の中からr個を選んで取り出す、組合せの総数を計算します。
組合せの計算
組合せの計算について
全体の数(n個)と選んだ数(r個)を入力し「組合せを計算」ボタンをクリックすると、n個の中から重複しないでr個を選んで取り出す組合せの総数を計算して表示します。
また、組合せの総数を求める計算方法も表示します。
全体の数と選んだ数は10,000までの正の整数で入力してください。
組合せとは
組合せとは、区別可能な異なるものの中から、いくつかを選んで取り出すことです。
組合せの総数は、nCrと書いて、全体の数(n個)から選んだ数(r個)の組合せの総数を表します。
nCr = n個からr個を選んで取り出したときの組合せの総数
例えば、A、B、C、Dの4つのアルファベットから、3つを選ぶとします。
このときの選び方は、「ABC、ABD、ACD、BCD」の4通りになります。
組合せでは順列と違って順番を考えないので、ABCとCBAといった並び替えて同じになる組合せは1つとして考えます。
A、B、C、Dから3つを選んだ場合の組合せを樹形図にするとこのようになります。
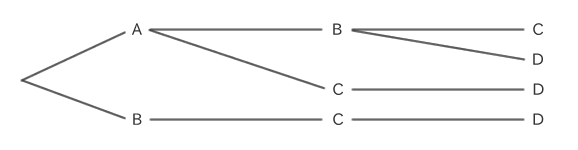
組合せの計算方法
組合せの総数を計算する場合、順列のように順番に並べたときの総数を同じ組み合わせの数で割って計算します。
例えば、A、B、C、Dの4つのアルファベットがあり、この中から3つを選んで組合せを考えるとします。
順列での並べ方の総数は4×3×2で24通りになります。
しかし順列では「ABC、ACB、BAC、BCA、CAB、CBA」の6通りの並べ方は、組合せでは順番を考えないので1通りになります。
なので組合せは、順列での並べ方の総数の24を6で割って4通りになります。
同じ組合せになるのは選んだ数の順列なので、3つを選ぶ場合は3!で6通りになります。
よって、n個からr個を選んで取り出す組合せの総数はnPrr!で計算できます。
また、nPr = n!(n−r)!なので、nPrr! = n!(n−r)! × 1r! = n!r!(n−r)!になります。
組合せの総数の公式
nCr = nPrr!
nCr = n!r!(n−r)!
またn個からr個を選ぶということは、n個から残りの(n−r)個を選ばないということと同じになります。
なのでr個を選ぶ組合せの総数と(n−r)個を選ぶ組合せの総数は同じになり、nCrとnC(n−r)は等しくなります。
nCr = nC(n−r)